Students Support
[ez-toc] Online MSc in Mathematics Online MSc in Mathematics course is 2 years post-graduate which is a branch of mathematics
[ez-toc]
| Level | Postgraduate |
| Degree | Master of Science |
| Minimum qualification | Bachelor’s degree with mathematics |
| Course duration | 2 years |
| Average Fees | INR 6000/- to INR 80,000/- per year |
| Starting Salary range | INR 400000 to INR 700000 |
| Exam Name | Conducting Body | Exam Date |
|---|---|---|
| IIT JAM Mathematics | IITs | February |
| ISI Admission Test | ISI Kolkata | May |
| CUCET | Central Universities | September |
| TIFR GS | Tata Institute of Fundamental Research | December |
| BHU PET Mathematics | Banaras Hindu University | May |
| DUET Mathematics | University of Delhi | June |
| JNU CEEB | Jawaharlal Nehru University | September |
| NEST Mathematics | NISER Bhubaneswar and UM-DAE CEBS Mumbai | June |
| KVPY-SA | Department of Science and Technology (DST) | November |
| JAMMU University Entrance Exam for MSc Mathematics | University of Jammu | June |
College Name |
Location |
Fees (approx.) |
|---|---|---|
| Indian Institute of Technology Bombay | Mumbai, Maharashtra | Rs. 20,000 – Rs. 80,000 per year |
| Indian Institute of Technology Delhi | New Delhi | Rs. 20,000 – Rs. 90,000 per year |
| Indian Institute of Technology Madras | Chennai, Tamil Nadu | Rs. 20,000 – Rs. 70,000 per year |
| Indian Statistical Institute | Kolkata, West Bengal | Rs. 9,000 – Rs. 29,000 per semester |
| University of Delhi | Delhi | Rs. 10,000 – Rs. 30,000 per year |
| University of Hyderabad | Hyderabad, Telangana | Rs. 10,000 – Rs. 25,000 per semester |
| Chennai Mathematical Institute | Chennai, Tamil Nadu | Rs. 4.5 lakhs per year |
| Harish-Chandra Research Institute | Allahabad, Uttar Pradesh | Rs. 10,000 – Rs. 50,000 per year |
| Institute of Mathematics and Applications | Bhubaneswar, Odisha | Rs. 50,000 – Rs. 1.25 lakhs per year |
| Ramakrishna Mission Vivekananda University | Belur, West Bengal | Rs. 18,000 – Rs. 30,000 per semester |
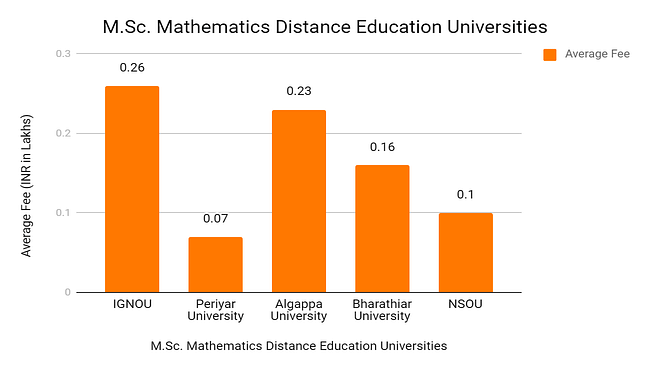
Semester I |
Semester II |
|---|---|
| Theorems on Principle, Maximal and Prime Ideals | Recapitulation: Rings, Some Special Classes of Rings |
| The Riemann – Stieltjes Integral | Phragmen-Lindel of theorem |
| Isomorphism Theorems and its Related Problems | Alexandroff ’s One Point Compactification |
| Finite and Infinite Sets | First-Order Partial Differential Equations |
| Linear Differential Equations of nth Order | Second-Order Partial Differential Equations |
| Modeling with Recurrence Relations with Examples of Fibonacci Numbers | The Conjugate Space H* of a Hilbert Space |
Semester III |
Semester IV |
| Calculus on Euclidean Space | Lebesgue Integral |
| Volterra and Fredholm Integral Equations | Convergence Theorems and Lebesgue Integral |
| Two-dimensional Flows of Inviscid Fluids | Riemannian Metric. Connections. Riemannian Connections and their Components |
| Numerical Solution of Partial Differential Equations | Partitions: De?nition of Partition of a +ve Integer |
| Meaning of First and Second-order Ordinary Derivatives | Asymptotic Values and Asymptotic Curves |
| Abstract Group Theory | Planarity:- Plane and Planar Graphs |
| Subject | Description |
|---|---|
| Real Analysis | Foundations of calculus and analysis, including limits, continuity, differentiability, and integration |
| Complex Analysis | Study of complex functions, including analytic functions, conformal mappings, and singularities |
| Abstract Algebra | Study of algebraic structures such as groups, rings, and fields |
| Linear Algebra | Study of linear equations and matrices, including vector spaces, linear transformations, and eigenvalues/eigenvectors |
| Differential Equations | Study of ordinary and partial differential equations, including existence and uniqueness theorems, solution techniques, and applications |
| Numerical Analysis | Study of numerical methods for solving mathematical problems, including interpolation, approximation, and numerical integration |
| Topology | Study of the properties of geometric shapes that are preserved under continuous transformations |
| Probability Theory and Stochastic Processes | Study of probability, random variables, and stochastic processes, including applications in statistics and financial mathematics |
| Number Theory | Study of the properties of integers and related mathematical objects, including prime numbers, Diophantine equations, and cryptography |
| Mathematical Modeling and Optimization | Study of the use of mathematical models to describe and solve real-world problems, including optimization techniques and applications in various fields |
| Book Title | Author(s) | Description |
|---|---|---|
| Principles of Mathematical Analysis | Walter Rudin | A classic textbook on real analysis, covering the basic concepts and results in detail |
| Abstract Algebra | Dummit and Foote | A comprehensive introduction to algebraic structures such as groups, rings, and fields |
| Linear Algebra | Friedberg, Insel, Spence | A thorough treatment of linear algebra, including vector spaces, linear transformations, and eigenvalues/eigenvectors |
| Partial Differential Equations | Lawrence C. Evans | A standard text on the theory and applications of partial differential equations |
| Probability and Random Processes | Geoffrey Grimmett and David Stirzaker | A comprehensive introduction to probability theory and stochastic processes |
| An Introduction to Numerical Analysis | Endre Süli and David Mayers | A thorough introduction to numerical methods for solving mathematical problems |
| Topology | James R. Munkres | A classic textbook on topology, covering basic concepts and theorems in point-set topology |
| Number Theory | Ivan Niven, Herbert S. Zuckerman, and Hugh L. Montgomery | A comprehensive introduction to number theory, including topics such as prime numbers, Diophantine equations, and cryptography |
| Elements of Optimization Theory | Thomas F. Coleman and Yuying Li | An introductory text on optimization theory and its applications |
| Mathematical Modeling in Continuum Mechanics | Roger Temam | A classic text on the use of mathematical models to describe and solve problems in continuum mechanics |
| Feature | MSc Mathematics | MSc Applied Mathematics |
|---|---|---|
| Focus | Pure Mathematics | Applied Mathematics |
| Coursework | Advanced Mathematics topics | Applied Mathematics topics with emphasis on their use in real-world problems |
| Skills Developed | Theoretical and analytical skills, problem-solving ability | Advanced mathematical modeling, quantitative analysis and problem-solving ability |
| Career Opportunities | Teaching and research positions in academia, government research organizations and private sector research labs | Opportunities in various industries, including finance, engineering, data science, and research organizations |
| Admission Requirements | Bachelor’s degree in Mathematics or related field with minimum required marks | Bachelor’s degree in Mathematics or related field with minimum required marks |
| Duration | 2 years | 2 years |
| Core Courses | Real Analysis, Algebra, Topology, Geometry, Differential Equations, Complex Analysis, Number Theory, Probability and Statistics | Partial Differential Equations, Applied Linear Algebra, Optimization, Numerical Analysis, Scientific Computing, Computational Methods for Applied Mathematics, Stochastic Processes |
| Elective Courses | Advanced Topics in Algebra, Advanced Topics in Analysis, Differential Geometry, Lie Groups and Lie Algebras, Algebraic Topology | Applied Stochastic Processes, Financial Mathematics, Graph Theory, Operations Research, Data Science, Machine Learning |
| Research Opportunities | Opportunities to conduct original research and publish papers in academic journals | Opportunities to work on real-world problems in collaboration with industry partners and apply mathematical modeling and analysis techniques to solve them |
| Scope for Further Studies/Research | Opportunities to pursue a PhD in Mathematics or related fields | Opportunities to pursue a PhD in Applied Mathematics, Engineering, Data Science or other related fields |
| Job Profiles | Approx Annual Average Salary |
| Research Scientist | INR 7 Lakhs |
| Economist | INR 7 Lakhs |
| Accountant | INR 2.6 Lakhs |
| Professor | INR 12 Lakhs |
| Business Analyst | INR 8 Lakhs |
| Quantitative Risk Analyst | INR 18 Lakhs |
| Equity Analyst | INR 5.8 Lakhs |
| Company | Industry |
|---|---|
| Indian Space Research Organisation (ISRO) | Space technology |
| Defense Research and Development Organization | Defense research and development |
| Indian Statistical Institute (ISI) | Research and development |
| National Institute of Science Education and Research (NISER) | Education and research |
| Tata Institute of Fundamental Research (TIFR) | Education and research |
| National Aeronautics and Space Administration (NASA) | Space technology and research |
| Council of Scientific and Industrial Research (CSIR) | Research and development |
| Amazon | E-commerce |
| Microsoft | Information technology |
| Information technology | |
| IBM | Information technology |
Unit no 303,3rd Floor, MBC , #134 Infantry Road, Bangalore- 560001
+91 9945744005
info@unitedcorrespondencecollege.in
Get Assistance Now!